Resistors in Series and Parallel Combinations – Explanation and Examples

In this article, we will discuss the combination of resistors – the series combination of resistors, and the parallel combination of resistors.

In an electrical or electronic circuit, we combine resistors in the following two ways to achieve the desired value of resistance-

• Series connection of resistors
• Parallel connection of resistors

Series Combination of Resistors

In a circuit, when resistors are connected end to end so that there is only one path for electric current to flow is called a series combination of resistors.

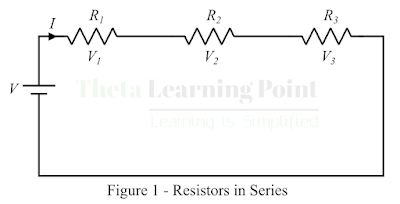
Consider a circuit as shown in figure-1 having three resistors R₁, R₂, and R₃ are joined end to end, i.e. the ending terminal of the first resistor is connected to the starting terminal of the second resistor, and the ending terminal of the second resistor to the starting end of the third resistor, so that current flowing through all the resistors is the same.

According to Ohm’s law, the voltage across various resistors is given by,

`\V_1=IR_1`

`\V_2=IR_2`

`\V_3=IR_3`

If V is the total voltage across the series combination of resistors, then we have,

`\V=V_1+V_2+V_3`

`\⟹V=IR_1+IR_2+IR_3`

`\⟹V=I(R_1+R_2+R_3 )`

`\V/I=R_1+R_2+R_3`

But, V/I is the total resistance of the series combination of resistors, i.e.

`\R_t=V/I`

`\∴R_t=R_1+R_2+R_3"     "…(1)`

Hence, from equation (1), it is clear that when a number of resistors are connected in series, the total resistance of the combination is equal to the sum of the resistance of the individual resistors.

If we have an electric circuit consisting of N resistors connected in series, then the total resistance of the circuit is given by,

`\∴R_t=R_1+R_2+R_3+⋯+R_N"     "…(2)`

Consider a special case, where a circuit consists of N resistors having equal values of resistance (say R), and are connected in series, then the total resistance of the combination is given by,

`\R_t=R+R+R+⋯"till "N`

`\∴R_t=NR"    "…(3)`

Hence, when a number of resistors of equal resistance value are connected in series, the total resistance of the combination is equal to the product of the number of resistors and the resistance of any one of the resistors.

Parallel Combination of Resistors

When one end of each resistor is connected to a common point and the other end of each resistor is connected to another common point so that the number of paths for current to flow is equal to the number of resistors, then it is called a parallel combination of resistors.

Consider a circuit as shown in figure-2 having three resistors R₁, R₂, and R₃ connected in parallel.

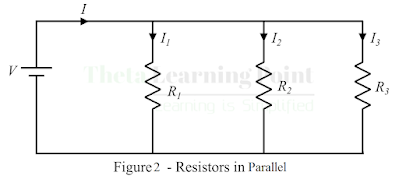
Here, the voltage across each resistor is the same, i.e. V, but the total current I divides into three parts, i.e. I₁ through the resistor R₁, I₂ through the resistor R₂, and I₃ through the resistor R₃. Hence, it is clear that in a parallel combination of resistors, there are as many current paths as the number of resistors.

According to Ohm’s law, the current flowing through each resistor is given by,

`\I_1=V/R_1`

`\I_2=V/R_2`

`\I_3=V/R_3`

Also, the total current I is given by,

`\I=I_1+I_2+I_3`

`\⟹I=V/R_1 +V/R_2 +V/R_3`

`\⟹I=V(1/R_1 +1/R_2 +1/R_3)`

`\⟹I/V=1/R_1 +1/R_2 +1/R_3`

But, V/I is the total resistance R_t of the combination.

`\∴1/R_t =I/V`

Therefore,

`\1/R_t =1/R_1 +1/R_2 +1/R_3"      "…(4)`

Hence, when a number of resistors are connected in parallel, then the reciprocal of total resistance is equal to the sum of the reciprocals of the individual resistors.

Case 1 – Two Resistors in Parallel:

Consider a circuit that contains two resistors connected in parallel as shown in figure-3. In this circuit, the total current I divides into two parts – I₁ through the resistor R₁, and I₂ through the resistor R₂. Then, the total resistance of the combination is given by,

`\1/R_t =1/R_1 +1/R_2`

`\⟹1/R_t =(R_2+R_1)/(R_1 R_2 )`

`\∴R_t=(R_1 R_2)/(R_1+R_2 )"     "…(5)`

Hence, the total resistance of two resistors in parallel is equal to the product divided by the sum of the resistances of the two resistors.

Case 2 – N Resistors of Equal Resistance in Parallel:

When N resistors of equal resistance (say R) are connected in parallel, the total resistance of the combination is given by,

`\R_t=R/N`

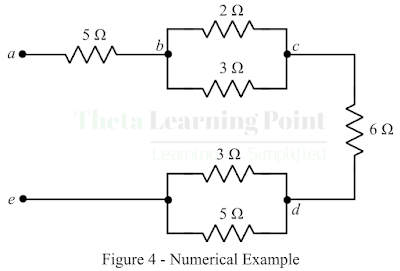
Numerical Example – Find the total resistance of the circuit shown in figure-4.

Solution –

Step 1: Resistance between points b and c:

`\R_(bc)=(2×3)/(2+3)=1.2 Ω`

Step 2: Resistance between points e and d:

`\R_(ed)=(3×5)/(3+5)=1.875 Ω`

Step 3: Resistance between points a and e, which is the total resistance of the network:

`\R_t=5+1.2+6+1.875`

`\∴R_t=14.075 Ω`

Conclusion

Thus, in this article, we discussed series and parallel combinations of resistors. From the above discussion, we can conclude that when a number of resistors are connected in series, then the total resistance of the combination is given by the sum of resistances of the individual resistors. The total resistance of the series combination is greater than the largest of the resistances.

When a number of resistors are connected in parallel, then the reciprocal of the total resistance of the combination is equal to the sum of reciprocals of resistances of the individual resistors. Also, the total resistance of the parallel combination of resistors is less than the smallest of the resistors.